
Average Runtime, Stacks, Queues
CSE-250 Fall 2022 - Section B
Oct 3, 2022
Textbook: Ch. 7
Stacks
A stack of objects on top of one another.
- Push
- Put a new object on top of the stack
- Pop
- Remove the object on top of the stack
- Top
- Peek at what's on top of the stack
Queue
Outside of the US, "queueing" is lining up.
- Enqueue
- Put a new object at the end of the queue
- Dequeue
- Remove the next object in the queue
- Head
- Peek at the next object in the queue
Thought question: How could you use an array to build a queue?
ArrayBuffer Attempt 1
- Enqueue
- Append
- Dequeue
- Remove(0)
What's the complexity?
ArrayBuffer Attempt 2
- Enqueue
- Insert(0)
- Dequeue
- Remove(last)
What's the complexity?
Can we avoid having to move all of the
elements forward or backward a spot?
ArrayDequeue (Resizable Ring Buffer)
Active Array = [start, end)
- Enqueue
- Resize buffer if needed
- Add new element at buffer[end]
- Advance end pointer (wrap around to front)
- Dequeue
- Remove element at buffer[start]
- Advance start pointer (wrap around to front)
What's the complexity?
Applications of Stacks and Queues
- Stack: Checking for Balanced Parenthesis/Braces
- Queue: Scheduling Packets for Delivery
- Both: Searching Mazes
Balanced Parenthesis/Braces
What does it mean for parenthesis/braces to be balanced?
- Every opening symbol is matched by a closing symbol
- No nesting overlaps (e.g., {(}) is not ok).
| {()({})} | {()) | ()) |
| ✅ | ❌ | ❌ |
Balanced Parenthesis/Braces
Idea: Count the number of unmatched open parens, braces.
Increment counter on (, decrement on )
Problem: allows {(})
Balanced Parenthesis/Braces
Idea: Track nesting on a stack!
On ( or {, push the symbol on the stack.
On ) or }, pop the stack and check the popped symbol.
Network Packets
- Router: 1gb/s internal network, 100mb/s external
- 1gb/s sent to router, but only 100mb/s can leave.
- How do packets get delivered?
- Queues
- Enqueue data packets in the order they are received.
- When outgoing bandwidth available, dequeue and send.
- Avoiding Queueing Delays
- Limit size of queue; Packets that don't fit are dropped
TCP: blocked packets are retried UDP: application deals with dropped packets.
Mazes
- O is the start, X is the objective
- There may be multiple paths
- Generally, we want the shortest
- Approach 1: Take the first available route in one direction
- Right, Down, Left, or Up
- Down, Right, Up, Left
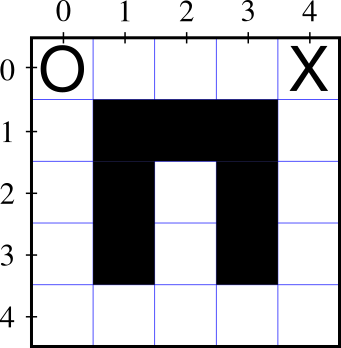
Mazes
- O is the start, X is the objective
- There may be multiple paths
- Generally, we want the shortest
- Approach 1: Take the first available route in one direction
- Right, Down, Left, or Up
- Down, Right, Up, Left
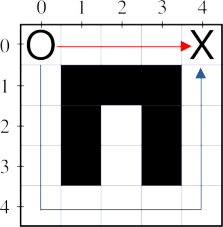
Mazes

How do you know which one is best?
Other problems with this algorithm?
Mazes
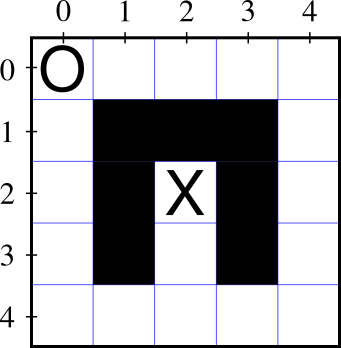
Mazes
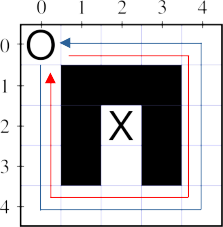
Priority order doesn't guarantee exploring the entire maze
Formalizing Maze-Solving
Inputs:
- The map: An $n\times m$ grid of filled/empty squares.
- The O is at position $start$
- The X is at position $dest$
Goal:
How do we define $steps$?
Formalizing Maze-Solving
Formalizing Maze-Solving
Formalizing Maze-Solving
Formalizing Maze-Solving
where...
$min\_adjacent(\texttt{pos}, \texttt{dest}) = $ $$\min\begin{cases} steps(moveRight(\texttt{pos}), \texttt{dest})\\ steps(moveDown(\texttt{pos}), \texttt{dest})\\ steps(moveLeft(\texttt{pos}), \texttt{dest})\\ steps(moveUp(\texttt{pos}), \texttt{dest})\\ \end{cases}$$
$steps(\texttt{pos}, \texttt{dest})$
- if pos == dest then return 0
- elif is_filled(pos) then return ∞
- else return 1 + min of
- $steps(moveRight(\texttt{pos}, \texttt{dest}))$
- $steps(moveDown(\texttt{pos}, \texttt{dest}))$
- $steps(moveLeft(\texttt{pos}, \texttt{dest}))$
- $steps(moveUp(\texttt{pos}, \texttt{dest}))$

Problem: Infinite loop!
Insight: A path with a loop in it can't
be shorter than one without the loop.
Mark nodes as visited
$steps(\texttt{pos}, \texttt{dest})$
- if pos == dest then return 0
- elif pos marked visited then return ∞
- elif is_filled(pos) then return ∞
- else
- Mark pos as visited
- return 1 + min of all 4 steps

Problem: The first time you visit a node,
it may be via a longer path!
Unmark nodes as you leave them
$steps(\texttt{pos}, \texttt{dest})$
- if pos == dest then return 0
- elif pos marked visited then return ∞
- elif is_filled(pos) then return ∞
- else
- Mark pos as visited
- stepCount = 1 + min of all 4 steps
- Unmark pos as visited
- return stepCount
Maze-Solving
Inputs:
- The map: An $n\times m$ grid of filled/empty squares.
- The O is at position $start$
- The X is at position $dest$
Goal:
What path did we take?
Idea:
Follow the nodes marked visited$steps(\texttt{pos}, \texttt{dest}, \texttt{visited})$
- if pos == dest then return visited.copy()
- elif pos ∈ visited return no_path
- elif is_filled(pos) then return no_path
- else
- visited.append(pos)
- bestPath = min of all 4 one-step paths
- visited.removeLast()
- return bestPath
$steps(\texttt{pos}, \texttt{dest}, \texttt{visited})$
- if pos == dest then return visited.copy()
- elif pos ∈ visited return no_path
- elif is_filled(pos) then return no_path
- else
- visited.push(pos)
- bestPath = min of all 4 one-step paths
- visited.pop()
- return bestPath
Thought question: Can you solve a maze
with a queue instead?